신규 블로그를 만들었습니다!
다이나믹 프로그래밍 DP
Dinamic Programing, 다이나믹 프로그래밍이란...
문제를 한번만 푸는 알고리즘
쉽게 생각하면, 점화식을 생각하면 된다.
중학교 수학을 배우면서
우리는 점화식에 대해 배운다.
예를들어...
a[n] = a[n-1] + 3a[n-2];
위와 같은 점화식처럼,
어느 n번째 부분만 문제를 풀어서 문제를 해결한다.
이와 같은 대표적인 예제로 피보나치 수열이 있다.

▲ (출처: http://www.softqt.com/softqt/board.php?board=research2&command=body&no=23)
피보나치 수열
1 1 2 3 5 8 13 21 34 55 ......
n번째 숫자 = (n-1)번째 숫자 + (n-2)번째 숫자
피보나치 수열을 구현해보자
보통 다이나믹 프로그래밍을 할때는 재귀함수를 사용한다.
사람이 이해하기도 편하고, 구현하기가 편하다.
코드 구현
#include <stdio.h>
// 1 1 2 3 5 8 13 21 ......
int fibonacci(int x){
if(x <= 2){
return 1;
}
return fibonacci(x-1) + fibonacci(x-2);
}
int main(void){
printf("%d ", fibonacci(10));
return 0;
}

메모이제이션 Memoization
사실 위와 같은 코드는 문제가 있다.
이미 계산한 내용을 또 다시 계산을 하기 때문에
필요없는 연산이 생긴다.
예를들어,
n = 5 일때,
fibo(1)
fibo(2)
fibo(1) + fibo(2)
fibo(2) + (fibo(1) + fibo(2))
(fibo(1) + fibo(2)) + (fibo(2) + (fibo(1) + fibo(2)))
위와 같이 전에 계산한 값을 매번 다시 계산을 한다.
n이 매우 커질 경우
오버헤드가 너무 크다.
실제로 n = 30을 넣어보면,
결과가 안나오거나 느리게 나오는 것을 알 수 있다.
계속 계산을 수행하고 있지만, 연산량이 너무 많아서 그렇다.
이때, 메모이제이션 방법을 사용한다!
이미 계산한 내용들을 저장해두고,
다시 연산 할 필요없이 저장된 데이터를 불러오는것이다.
data[1] = fibo(1)
data[2] = fibo(2)
data[3] = data[1] + data[2] = fibo(3)
data[4] = data[2] + data[3] = fibo(4)
data[5] = data[3] + data[4] = fibo(5)
공간을 조금 더 사용해서 데이터를 저장해두면(기억을 하면)
연산량을 대폭 줄일 수 있다.
메모제이션을 안쓰면, 시간복잡도는 O(2^N)이다.
n이 커질수록 어마어마하게 시간이 오래걸린다는것을 알 수 있다.
하지만, 메모제이션 방법을 사용하면 시간복잡도는 O(N)으로 급격히 줄어든다.
코드 구현
#include <stdio.h>
// 0으로 초기화 되어있다.
int data[100];
// 1 1 2 3 5 8 13 21 ......
int fibonacci(int x){
if(x <= 2){
return 1;
}
if(data[x] != 0){
// 이미 계산을 해서 값이 가지고 있다.
return data[x];
}else{
// 0이라는 것은 아직 계산이 된적이 없다는 것...
// 계산을 하고 저장해둔다.
// 그리고 값을 반환한다.
data[x] = fibonacci(x-1) + fibonacci(x-2);
return data[x];
}
}
int main(void){
printf("%d ", fibonacci(30));
return 0;
}
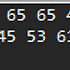
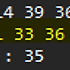
결과확인

30번째 수를 구한 결과
관련 글
2018/05/02 - [Algorithm/백준 온라인 저지] - 백준/11726번 :: 타일링 (C/C++ 구현)
2018/05/02 - [Algorithm/백준 온라인 저지] - 백준/11727번 :: 2xn 타일링 2 (C/C++ 구현)
'Algorithm' 카테고리의 다른 글
| 자료구조 :: JAVA를 이용한 힙 정렬 (Heap sort) 힙 소트 (2) | 2018.05.03 |
|---|---|
| 자료구조 :: JAVA를 이용한 퀵 정렬, Quick Sort, 퀵 소트 (JAVA 구현) (3) | 2018.05.02 |
| 알고리즘 :: 이진트리와 순회 전위순회(preorder), 중위 순회(inorder), 후위 순회(postorder) C/C++ 구현 (6) | 2018.05.01 |
| 알고리즘 :: 크루스칼 알고리즘 Kruskal Algorithm (C/C++ 구현) (3) | 2018.05.01 |
| 알고리즘 :: Union Find(Disjoint-Set) 알고리즘, 합 집합 찾기 알고리즘 (C/C++ /JAVA 구현) (4) | 2018.04.30 |




최근댓글